• After 15+ years, we've made a big change: Android Forums is now Early Bird Club. Learn more here.

I need a math wizzard

Puddy Tat

Puddy Tat

Well-Known Member
I need a math wizard. There are a lot of smart people here so I thought it would be a place to ask. Nothing to do with Android so to keep from plugging up the forum if one could PM me I have a problem for you.
 
Let us know what the problem is. I'm sure one of us will figure it out. BTW, I moved this to the lounge where we keep our non android off topic posts.:)
 
Thanks for the move. That is why I could not find it, it is way past the phones.
.
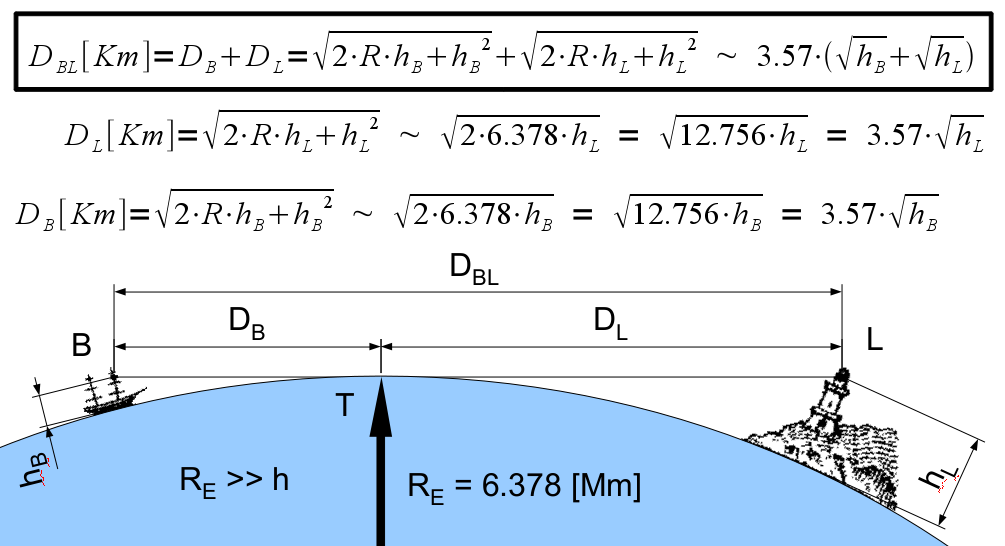
You have a dish or directional antenna on top of an 80 foot tower. The other dish to receive is 14.3 miles away. How high would that tower need to be so these dishes could line of sight "see" each other.
 
I thought you were going to ask about trains leaving from Pittsburgh and Boston at various speeds and where would they meet.:D
 
I assume this is supposed to take into account the earths curvature?

Is this math homework or a real world problem :rofl:
 
If that is correct, then for two objects 14.3 miles apart, 9'6" of height needs to be gained by one of the two objects assuming no trees, hills, or houses. How high is the other end of this line of sight equation.
 
Unforgiven said:
If that is correct, then for two objects 14.3 miles apart, 9'6" of height needs to be gained by one of the two objects assuming no trees, hills, or houses. How high is the other end of this line of sight equation.
Click to expand...

Thats why the problem doesn't really make sense, if one is 80 feet up, you could still see it from the ground even 120 miles away... right?

(80 feet) * (12in/ft) / (8 in/mi) =

That seems really far
 
Yeah, I found that calculator, and it would put 80' just out of range if line of sight at 13 miles. I also found an antenna calculator sit that came up with roughly the same number. I'm not sure that 8 inches per mile is correct. I think at this point it is real important to know how high the other tower is.
 
Yeah, on that calculator it would be between 1-2 feet for a 14.3 mi line of sight.

It doesn't get exact enough
 
Unforgiven said:
I thought you were going to ask about trains leaving from Pittsburgh and Boston at various speeds and where would they meet.:D
Click to expand...
That one is simple. The one that goes fastest meets first.:rolleyes:

Rxpert83 said:
I assume this is supposed to take into account the earths curvature?

Is this math homework or a real world problem :rofl:
Click to expand...
Yes the curve.
A question a friend ask me.

Rxpert83 said:
This seems like it'll help you:
https://answers.yahoo.com/question/index?qid=20080319041236AAz7drc

:)
Click to expand...
Yup. That calculation bummed me out. But the 8 inches made sense.
 
OK, so I reread the question and the goal is to figure out the height of the second antenna. Using the calculator I linked above, you would be able to achieve 15 miles of line of sight with one tower at 80' and the second at 2'. That calculator doesn't take into account trees, hills, or mountains. If there is a city in between, then line of site will be obstructed. 2' seems like underkill. If the other end is at the peak of a roof (say 20') then you get line of sight to 19 miles.
 
Again, that works because they are dealing with an oil rig on water. So the only obstructions would be waves and / or a passing ship.:dontknow:
 
WOW! So many math wizards here I can not type that fast.
That was the entire question: Tower no1 is 80 feet. For this antenna to line of sight "see" the other antenna, how high would the "other" tower need to be.
 
Puddy Tat said:
WOW! So many math wizards here I can not type that fast.
That was the entire question: Tower no1 is 80 feet. For this antenna to line of sight "see" the other antenna, how high would the "other" tower need to be.
Click to expand...

The link I first gave was wrong, and using the calculator unforgiven posted we can see that tower 2 has to be somewhere between 1-2 feet high

Now according to wikipedia lol
Horizon - Wikipedia, the free encyclopedia


With d in miles and h in feet
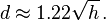
09c3a696f80a0d375ba87cd30b15a94f.png



We've discovered I'm no math expert. Bowing out now haha
 
Well, this gives me an idea to pass on to my friend. I'll tell him to climb up to his roof top (22 feet) at night and find out what he can see from there. If he is over the trees and can see some other towers with lights at about the same distance that just may give him what he wants to know.
.
Thanks for all the math answers.:)
.
PT
 
It's all pretty simple really ...

HorizonDistance.png


:eek::eek::eek::eek::eek::eek::eek::eek:

Oh and pup, about those trains leaving Chicago and New York ...

Someone should have told them to use separate tracks. ;)
DutchTrainCrash.png
 
Good luck Puddy Tat. If your friend want's help, us two clowns math wizzards will be gald to help if he signs up.:D
 
Well, he is not much of a computer person. Turns it on about once a week for a short time. I will pass all this on.
 
I think the solution is very simple, you need to use pythagoras and proportionality. Between the two objects there is two right-triangles and hence you can use pythagoras to calculate the high which is needed. But you also need proportionality because you know the distance between the two objects along the ground (not through air). At first you need to calculate the sum for the angle of these two right-triangles (the angle in the center point of earth) and of course the angle in the center point of earth for the right-triangle related to the tower by using trigonometry. Then you can use proportinality to calculate the cathetus for the other right-triangle and finally calculate the missing hypotenuse. Of course this assumes that earth is the perfect ball and between the two objects the line is a tangent touching the surface of earth.

Or am i missing something... it's 3am already and this is not the best time to think about math without a paper and a pen :D

Edit. A quick explanation...
etemaser.jpg


Please feel free to try numbers! Ill check that later, now i need to hurry..........
 
You must log in or register to reply here.
Back
Top Bottom