Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
-
After 15+ years, we've made a big change: Android Forums is now Early Bird Club. Learn more here.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
6
- Thread starter Vihzel
- Start date
alostpacket
Over Macho Grande?
i just wonder
let x=1, y=2
2x
Here is the answer: YouTube - 6
DaSchmarotzer
Blame it on me
Here is my reply to that:
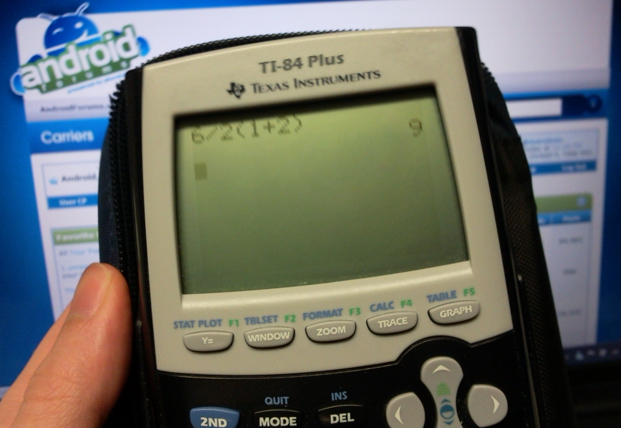
Read the thread if you haven't already for explanations. Welcome to the forums by the way!
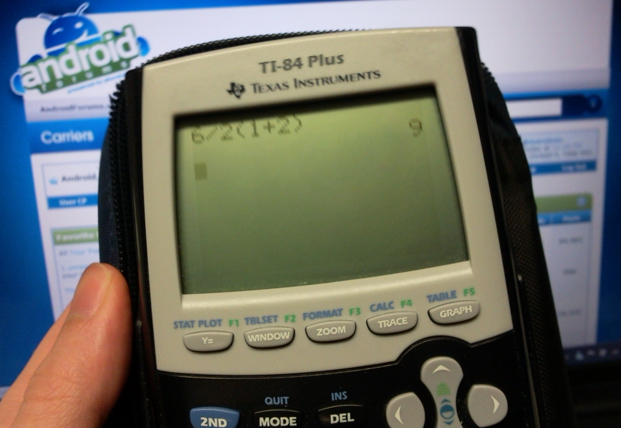
Read the thread if you haven't already for explanations. Welcome to the forums by the way!

Check's in the mail!
Roze
Hiding behind a mystery
I think I've brought a lot of people to Android Forums (whether they make an account or not) based off of this thread. lol I assume a lot of people typed it in Google and this site came up as a link.
... I should be paid. That's all.
You're nowhere near Fex though
 I think he got a platoon to join AF, lol, just so they can post in his thread.
I think he got a platoon to join AF, lol, just so they can post in his thread.I brought in eleventeen.
susanlai89
Lurker
‎6
XplosiV
Master X is Watching You
‎6
Order of operations - Wikipedia, the free encyclopedia
Scroll down to "Gaps in the Standard."
What this section states (or implies) is that if you try to interpret 6
novox77
Leeeroy Jennnkinnns!
The only other thing I have to say on the matter is to correct those among you who think that left/right has any precedence. IT DOESN'T MATTER AT ALL.
Glad you agreed with my previous post (even though I'm sure many people don't). But I'm not sure I agree with your above statement without some clarification. 6
I'm no longer at all interested in the original question, as it's an interpretation question: basically does the (x+y) term belong to the numerator or denominator. This is the difference between evaluating to 9 and to 1, respectively. The problem is it's missing a set of parentheses and left up to the reader to decide where they ought to fit.
I can assure you, left and right has absolutely no precedence because of the commutative property of addition and multiplication. Since subtracting term y from term x (seen as (x-y))is nothing more than the addition of the negative value of term y to term x (seen as (x+(-1)*y)), we can force subtraction to commutativity through addition. Similarly, division can be forced to commutativity through the use of fractions and multiplication (yes, this doesn't completely remove the need for division, but it does help me in what I'm looking to illustrate).
Once we have reached this, we can work through (useful iterations) of this type of problem from left to right, from right to left, or from the centre out if desired as long as we remember to give good respect to the order of operations (and though it has been stated a couple of times already, I think it merits repeating that multiplication and division are on an equal order, as are addition and subtraction (this is why we see several different flavours of PEMDAS)).
To me, left-to-right takes precedence, so 9 is the only correct answer.
I can assure you, left and right has absolutely no precedence because of the commutative property of addition and multiplication. Since subtracting term y from term x (seen as (x-y))is nothing more than the addition of the negative value of term y to term x (seen as (x+(-1)*y)), we can force subtraction to commutativity through addition. Similarly, division can be forced to commutativity through the use of fractions and multiplication (yes, this doesn't completely remove the need for division, but it does help me in what I'm looking to illustrate).
Once we have reached this, we can work through (useful iterations) of this type of problem from left to right, from right to left, or from the centre out if desired as long as we remember to give good respect to the order of operations (and though it has been stated a couple of times already, I think it merits repeating that multiplication and division are on an equal order, as are addition and subtraction (this is why we see several different flavours of PEMDAS)).
I have to first determine what the divisor is: 2 or the quantity 2*3.
And this is exactly why this poorly iterated problem is undergoing such a long debate. This numerator or denominator question is the ambiguous part you were alluding to earlier. It's an interpretation question. But remove the ambiguity by adding a set of parentheses around one term or another, and it's all good. This particular problem is written badly, but I still insist that left and right are no higher order than each other.
Order is irrelevant once everything is converted to multiplication and/or addition, but before that can be done, order IS affecting that conversion...
So it isn't a question of order, it's just that this problem is badly written and open to a couple of conflicting interpretations.
DaSchmarotzer
Blame it on me
This particular problem is written badly, but I still insist that left and right are no higher order than each other.
You should use only multiplications, since divisions are a multiplication of the inverse. Just like subtraction is the addition of negative numbers. Also, the algorithm computers use is left to right.

Have you read the whole thread? There are good replies out there.
I did indeed read the thread. There were a small handful of replies with decent content; the rest was pretty much chaff.
The reason computer algorithms evaluate left to right is that they were coded that way. One could just as easily code them to evaluate right to left. Or using a different notation entirely, like RPN.
The rest of what you said I agree with and also mentioned a couple of posts up.
The reason computer algorithms evaluate left to right is that they were coded that way. One could just as easily code them to evaluate right to left. Or using a different notation entirely, like RPN.
The rest of what you said I agree with and also mentioned a couple of posts up.
DaSchmarotzer
Blame it on me
I did indeed read the thread. There were a small handful of replies with decent content; the rest was pretty much chaff.
The reason computer algorithms evaluate left to right is that they were coded that way. One could just as easily code them to evaluate right to left. Or using a different notation entirely, like RPN.
The rest of what you said I agree with and also mentioned a couple of posts up.
Alright.

I know there are many notations, but the one used "by default" as a convention is usually left to right, that was the point I was trying to make.
Well, I think we're pretty much done with that topic then. What else is there to say?
XplosiV
Master X is Watching You
It seems to me that the answer is somewhat split between the simple folk and the math geeks. Ask anyone in the street and they will probably solve the question using left to right. where as ask anyone with some kind of higher education in math, and they will probably use the math parenthesis. Theres not a lot of point 'simplifying' the problem, the problem 'as is' done by a mathematician, using the common laws of math, will simply answer it as 1.
Who can tell me the highest number, that when written in the queens English, consists of only three words?
(IE 110 = one hundred and ten, 4 words)
Who can tell me the highest number, that when written in the queens English, consists of only three words?

(IE 110 = one hundred and ten, 4 words)
This thread wins 'Nerdiest thread in all of Phandroid' hands down.
Hush!!
Glad you agreed with my previous post (even though I'm sure many people don't). But I'm not sure I agree with your above statement without some clarification. 6
